この記事では、因果推論における「傾向スコア分析」について、その概要や適用可能なケース、実施におけるポイントを具体例をもとに解説します。
<目次>
傾向スコア分析とは
どのような分析手法なのか
「傾向スコア分析」は、ランダム化比較試験 (RCT) は実施できないものの、結果に影響を与える主な要因があらかじめ分かっている場合に、処置を受けるグループと受けないグループの間でそれらの要因に関してバランスを取り、RCTに近い状態を作り出すことで、処置効果を測定する手法です。
より具体的には、処置の割り当てと結果に影響を与える複数の要因をもとに、「各対象者が処置を受ける傾向性(確率)」を表す合成変数「傾向スコア (propensity score)」1を作成することで、傾向スコアが同じ対象者の間では、結果に影響を与える要因がバランスされた状態を作り出します。
これにより、傾向スコアの各値における両グループの結果の差を、処置の有無によるものと推定することが可能となります。対象者全体における処置効果は、後述するように、傾向スコアの値をもとにしたマッチングや層別解析、重み付けなどの調整を行うことで算出されます。
例えば、低所得家庭における子供の進学を支援する政策として、一定以下の所得の家庭を対象に、進学支援金を支給するケースを考えます。この時、支給対象は、全ての申請者の中から申請情報に基づいて一定数が恣意的に選ばれたとします。
この場合、「支援金の支給対象となるか否か」と相関する要因は、「子供の進学率」とも相関している可能性が高いため、支援金の支給を受けた家庭と受けなかった家庭の子供の進学率を単純比較することは、支援金の支給が進学率に与える効果を過大または過少に評価する可能性があります。
ここで仮に、子供の進学率が、家庭の所得金額、親の最終学歴、居住エリアの進学率、子供の学業成績、の4つの要素でほぼ説明可能であることが分かっているとします。
この時、これら4つの要素に関するデータをもとに、分析対象の全ての家庭について「支援金の支給対象へのなりやすさ」を表す傾向スコアを算出することで、同じスコアの値を持つ家庭における結果の差を、支援金支給の有無によるものと判断することが可能となります。
本来、4つの要素全てが同じ家庭のペアを見つけることは容易ではありませんが、傾向スコアという1つの数値に集約することでそれを容易に実現できる点が、傾向スコア分析の強みであると言えます。
作成:Intelligence In Society
どのような場合に適用できるのか
傾向スコア分析は、各対象者が処置を受ける確率を傾向スコアで表すことで、傾向スコアが同じ対象者の間では処置の有無がランダム(無作為)に決定されている、とみなせることを利用して、処置効果の推定を行う手法です。
上に挙げた例のように、政策や事業などが目的とする結果に影響を与える「処置以外の」要因として、年齢・学歴・年収・性別といった具体的な要因が特定されているケースで有効な推定方法です。
また、医学領域においては、特定の疾患に対する治療法の効果を測定する際に、治療による効果の推定にバイアスを生じさせる要因(交絡因子)の影響を可能な限り制御し、より適切な因果効果の推定を行うための手法として広く活用されています2。
一方で、結果に影響を与える主な要因の全てが傾向スコアに集約されていない場合、推定結果が誤ったものとなる可能性があり、そのような脱落要因がないことを説得力を持って説明することが必要となります。
その点から、ある結果の発生する構造が既にある程度解明され広く認知されているテーマや、分析者自身が長年の経験から、結果に影響する要因について深い実践知を持っているテーマなどに傾向スコア分析を活用することで、精度の高い処置効果の推定が可能になると言えます。
傾向スコア分析の実施におけるポイント
傾向スコア分析に必要な仮定
傾向スコアに基づく因果効果の推定が適切なものであるためには、「強い意味での無視可能な割付け (strongly ignorable treatment assignment)」3と呼ばれる条件を満たすことが必要です。この条件は、因果効果の推定に影響を与える変数がモデルから抜け落ちていることにより、推定結果にバイアスが生じることを意味する「脱落変数バイアス」が生じていないことを表します。
「強い意味での無視可能な割付け」の条件を満たすためには、具体的には以下の3つの仮定が満たされている必要があります。
①SUTVA (Stable Unit Treatment Value Assumption):
「SUTVA」とは、「個体ー処置(unit-treatment)の組み合わせに対する効果の値(value)が、一義的に定まる(stable)」という仮定であり、より簡潔には、「処置を受ける個体において、処置の効果が安定している」という仮定4を意味します。
SUTVA条件においては、「それぞれの個体が受ける処置の影響が、他の個体が受ける処置に影響されない」ことを意味する「No interference (No spillover)」と、「処置の状態を一義的に定義できる」ことを意味する「No hidden (multiple) version of treatment」の2つの要件が、共に満たされていることが必要とされています。
SUTVA条件についてのより詳細な解説は、以下のページをご覧ください。
②条件付き独立性(無交絡性):
「条件付き独立性」とは、共変量によって条件付けた時、処置の割り当てが無作為に行われたと考えることができることを意味します。これは、観測されている変数の他に、処置の割り当てに影響を与える変数が存在しないということを表します。
例えば、先ほどの進学支援金を支給するケースにおいて、「処置」である支援金の支給対象になるか否かに影響を与える要因が、家庭の所得金額、親の最終学歴、居住エリアの進学率、子供の学業成績の4つのみで、他には処置の割り当てに影響を与える要因が存在しないとします。
「条件付き独立性」は、この4つをもとに算出した「支援金の支給対象へのなりやすさ」を表す傾向スコアが同じ対象の間では、処置の割り当てが無作為に行われたと見なせることに該当します。
③条件付き正値性(オーバーラップ条件):
「条件付き正値性」とは、傾向スコアが「0より大きく、1より小さい」(0または1になってはいけない)ということを指します5。これは、ある共変量の値を持つ対象の「処置への割り当てられやすさ」が、0%(常に割り当てられない)または100%(常に割り当てられる)にならないことを意味します。
仮に、ある対象の傾向スコアが「1」(常に処置を受ける)となった場合、それは同じ傾向スコアを持ちながら「処置を受けない」対象が存在しないことを意味するため、両者の結果をもとに処置効果の推定を行うことができません。
作成:Intelligence In Society
これら3つの仮定が満たされるとき、「強い意味での無視可能な割付け」の条件が満たされます。その結果、傾向スコアが同じであれば、処置群と統制群の共変量の分布が同じである(=バランシングが成立している)と考えることができ、両グループの結果の差から処置効果を推定することが可能となります。
傾向スコアの算出
具体的な傾向スコアの算出において広く使用されるものが、ロジスティック回帰モデルです。「処置の対象へのなりやすさ」を傾向スコアとして算出する際、傾向スコアはその定義から「0~1」の間に収まる必要がありますが、これを、処置の割り当て有無を目的変数、共変量を説明変数とした線形回帰モデルで表した場合、目的変数の値は「0~1」の範囲を超えた値も取ってしまいます。
また、実際のケースにおいては、ある基準値を境に「支援金の支給対象となるか否か」の線引きが行われるように、処置の対象となる確率は、線形回帰モデルで表現されるように単調に増加していくのではなく、ある点を境に急激に増加(または低下)すると考えられます。
作成:Intelligence In Society
傾向スコアが持つこのような特徴をうまく近似できるのが、ロジスティック回帰モデルです。傾向スコアは、ロジスティック回帰モデルによって以下のように算出されます。
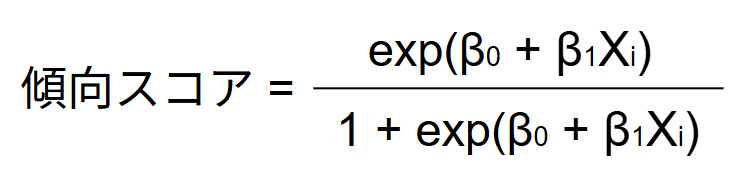
ここで、「exp(*)」は、自然対数の底eの*乗を指し、(*)内の数式は、処置の割り当て有無を目的変数、共変量を説明変数とした線形回帰モデルにあたります。ロジスティック回帰モデルは、説明変数によって作られる線形の関数の取る値を、目的変数の確率に変換していると理解することができます。
なお、傾向スコアのモデル化には、上記のロジスティック回帰モデル以外にも、確率変換に標準正規分布を使うプロビットモデルや、機械学習の手法を使う方法などが存在します。
傾向スコアによる因果効果の推定
算出した傾向スコアをもとに、処置による因果効果の推定を行います。傾向スコアをもとにした因果効果の推定方法には、主に以下の3つのアプローチがあります。
傾向スコアマッチング
1つ目は、傾向スコアが近い処置群と統制群の個体同士をマッチングさせてペアにし、両者の結果の差を処置効果とする方法です。
マッチングの方法には、傾向スコアの値が近い個体同士から順番にマッチングさせていく方法(最近隣法マッチング)や、マッチングされた全てのペア間の「平均的な近さ」が最も小さくなるようにする方法(最適ペアマッチング)などがあります。
マッチングでは、ペアの見つかった個体のみが残され、ペアの見つからなかった個体は計算から除外されます。また、処置群の個体に対して、統制群からマッチングする候補を選び、マッチング後のデータは処置群の個体を中心として構成されるため、マッチングによって推定できる因果効果は、処置群における平均処置効果 (Average Treatment Effect for Treated : ATT)となります5。
なお、最近隣法マッチングについては、ケースによっては処置群と統制群で共変量がバランシングしない状態を生じさせる可能性が指摘されており6、最適ペアマッチングがより望ましいとする考え方があります。また、最近隣法マッチングの実施の際には共変量が実際にバランシングしていることの確認などが必要とされています。
層別解析
2つ目は、傾向スコアの値によって対象を複数の層(5層~10層程度)に分け、層ごとに処置群と統制群が同じような傾向スコアを持ちバランシングされた状態を作ることで、処置効果の推定を行う方法です。
先の進学支援金を支給するケースでは、仮に4つの各共変量について5つずつの層に分ける場合、必要な層の数は5^4=625層となり、適切な分析には非常に大きなサンプルサイズが必要となります。これら4つの共変量の情報を集約した傾向スコアを使うことで、サンプルサイズがより少ない場合においても因果効果の推定が可能となります。
層別解析では計算に全てのデータを使用することから、推定できる因果効果は平均処置効果 (Average Treatment Effect : ATE) となります。ATEは、各層における「処置効果の平均値 × 全体に対する各層の個体数の割合」の値を合計することで算出されます。
逆確率重み付け法 (IPW)
3つ目は、傾向スコアの逆数を「重み」として用いてデータを拡張することで、共変量で条件付けた上での処置の割り当てについて「条件付き独立性」が成立する状況を作り、処置効果を推定する方法です。
具体的には、処置群の個体に対して「傾向スコアの逆数」、統制群の個体に対して「(1-傾向スコア)の逆数」を掛けることで、処置群と統制群の間で共変量(傾向スコア)のバランシングが成り立つ状態を作り出し、疑似的に無作為化実験 (RCT) に近い状態を作ります。
例えば、処置群の個体で傾向スコアが「0.1」の個体については「1 / 0.1 = 10」、統制群の個体で傾向スコアが「0.1」の個体については「1 / (1 – 0.1) = 1.11」を掛けます。これにより、処置群のうち、傾向スコアが低い希少な個体についてはその情報を大きく、逆に傾向スコアが高い個体についてはその情報を相対的に小さくした形で処置効果が推定されます。
作成:Intelligence In Society
なお、極端に小さい(または大きい)傾向スコアを持つ個体については、処置群または統制群に割り当てられる確率が非常に小さくなるため、その逆数として非常に大きな重みが与えられることになります。このような場合、外れ値となった一部の個体が結果に過度な影響を及ぼし、推定結果に悪影響を与える可能性があります。
このような場合への対処法として、事前に「カットオフ値」を設定し、この値を超える重みについては、カットオフ値に固定する方法(クリッピング)があります。
クリッピングは、外れ値をカットオフ値に固定することでその影響を制御し、推定結果の安定性を高める効果がありますが、一方で、データが持つ情報の一部を捨てることにより推定結果にバイアスを生じさせるリスクもあります4。クリッピングを行う際は、クリッピングあり/なしのそれぞれ方法で推定した結果を比較することで妥当性を検証するなどの対応が必要となります。
傾向スコア分析の強みと弱み
傾向スコア分析の強み
傾向スコア分析の強みは、RCTは実施できないものの、処置の割り当てと結果に影響を与える要因(交絡因子)が特定できている場合において、傾向スコアを利用することで処置が無作為に割り当てられたと見なせる状態を作りだすことができる点です。
特に、交絡因子が多数の場合、全ての交絡因子に関して同等の個体同士を処置群と統制群から見つけ出すことはほぼ不可能ですが、これを傾向スコアという1つの数値に集約することでそれを容易に実現できる点が、傾向スコア分析の大きな強みであると言えます。
そのため、ある結果の発生する構造が既にある程度解明され広く認知されているテーマや、分析者自身が長年の経験から、結果に影響する要因について深い実践知を持っているテーマなどに傾向スコア分析を活用することで、精度の高い処置効果の推定が可能になります。
傾向スコア分析の弱み
一方、傾向スコア分析の弱みは、傾向スコアで情報を集約することができるのは、あくまで「観測されている」交絡因子についてだけである点です。そのため、もし未観測の交絡因子が存在する場合は、傾向スコアが不適切なものとなり、これをもとに推定された結果はバイアスを含んだものとなります。
特に、傾向スコアをもとに個体に重み付けを行う逆確率重み付け法 (IPW)では、傾向スコアが正しく算出されていないことによって極端に大きな重みが生じている場合などにおいて、推定結果に悪影響が生じる可能性が懸念されます。
このようなIPWの弱みを補う手法として、IPWによる推定を回帰分析による推定と組み合わせ、より信頼性の高い推定を行う「Doubly Robust Estimation : DR」(二重に頑強な推定法)と呼ばれる手法も提案されています7。
DRでは、傾向スコアを算出するモデルと、結果変数を推定するモデルの2つのうち、いずれか一つが正しければ、適切な処置効果の推定が可能となるため、IPWにおいて傾向スコアが正しくないことにより生じるリスクを、一定程度軽減する効果が期待できます。
ここまで、因果推論における「傾向スコア分析」について、その概要や適用可能なケース、実施におけるポイントを解説しました。
本記事に関連するトピックについては、以下のページをご覧ください。
また、因果推論に関する全ての記事は以下のページからご覧いただけます。
参考文献・注記:
1. Rosenbaum, P. and Rubin, D. (1983) The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika, 70, 41-55.
2. Michael Webster-Clark, Til Stürmer, Tiansheng Wang, Kenneth Man, Danica Marinac-Dabic, Kenneth J Rothman, Alan R Ellis, Mugdha Gokhale, Mark Lunt, Cynthia Girman, Robert J Glynn (2021) “Using propensity scores to estimate effects of treatment initiation decisions: State of the science”, Statistics in Medicine, 40, 1718-1735
3. Guido W. Imbens, Donald B. Rubin. (2015) “Causal Inference for Statistics, Social, and Biomedical Sciences An Introduction”, Cambridge University Press
4. 金本拓 (2024) 『因果推論ー基礎から機械学習・時系列解析・因果探索を用いた意思決定のアプローチー』, オーム社
5. 高橋将宣(2022) 『統計的因果推論の理論と実装 ― 潜在的結果変数と欠測データ ― 』共立出版
6. Gary King, Richard Nielsen. (2019) “Why Propensity Scores Should Not Be Used for Matching”, Political Analysis 27 (4), 435-454
7. Michele Jonsson Funk, Daniel Westreich, Chris Wiesen, Til Stürmer, M Alan Brookhart, Marie Davidian (2011) “Doubly Robust Estimation of Causal Effects”, American Journal of Epidemiology, 173, 7, 761–767

























